Outil Optimisation
L’outil Optimisation peut résoudre les problèmes d’optimisation de la programmation linéaire (LP), la programmation linéaire en nombres entiers mixtes (MILP) et la programmation quadratique (QP) à l’aide de modes d’entrée de fichier, de matrice et manuels.
Cet outil utilise l’outil R. Allez dans Options > Télécharger les outils prédictifs et connectez-vous à la Portail Téléchargements et licences Alteryx pour installer l’outil R et les packages utilisés par ce dernier. Reportez-vous à la page Outil R. Voir Télécharger et utiliser les outils prédictifs.
Qu’est-ce que l’optimisation ?
L’optimisation a diverses applications dans de nombreux secteurs d’activité, par exemple les chaînes logistiques, le transport, les services financiers, la vente au détail, les télécommunications et l’énergie. Les domaines d’application incluent l’optimisation des chaînes logistiques, l’optimisation des assortiments, l’optimisation des portefeuilles, la planification de la main-d’œuvre et la programmation sportive.
Un problème d’optimisation se présente généralement sous la forme mathématique suivante, qui consiste en une fonction objectif (première équation), un ensemble de contraintes (deuxième équation), ainsi que la spécification des types (continu, entier, binaire) et des limites des variables de décision (troisième équation). Il convient généralement de trouver les valeurs des variables de décision qui optimisent ou minimisent l’objectif, tout en satisfaisant l’ensemble des contraintes, des types et des limites sous-jacents.
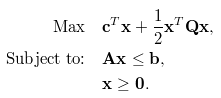
Connecter les entrées
Aucune entrée n’est requise pour les modes d’entrée de fichier ou manuel. Pour le mode d'entrée Matrix, les entrées O et A sont nécessaires, mais B et Q sont optionnels.
- O ancre: (requis pour le mode d'entrée de matrice) Utilisez cette entrée pour fournir les noms des variables de décision, leurs coefficients dans la fonction objective, et facultativement leurs limites et types.
- variable: (obligatoire) une chaîne, des noms de variable de décision. Correspond à x dans les équations.
- coefficient: (requis) un nombre, un coefficient de chaque variable de décision dans la fonction objective. Correspond à c.
- lb: (facultatif) nombre, limite inférieure de la variable de décision. La valeur par défaut est 0.
- UB: (facultatif) un nombre, limite supérieure de la variable de décision. La valeur par défaut est Inf (infini positif).
- type: (facultatif) un caractère, le type de la variable de décision, qui peut être C (continu), B (binaire) ou I (entier). La valeur par défaut est C.
- Une ancre: (nécessaire pour le mode d'entrée de la matrice) Utilisez cette entrée pour fournir la matrice de contrainte correspondant à A dans les équations. Vous pouvez organiser la matrice de deux manières différentes :
- Matrice dense:
- Contraintes dansles lignes: chaque ligne correspond à une contrainte. Le premier champ peut éventuellement être nommé contrainte pour indiquer le nom de la contrainte dans chaque ligne, tandis que les noms de champs restants doivent correspondre aux variables de décision définies dans O. En outre, vous pouvez inclure les champs dir et RHS pour lancer l' entrée B dans ce.
- Variables dansles lignes: chaque ligne correspond à une variable. Le premier champ doit être nommé variable, tandis que les noms de champs restants doivent correspondre aux noms de contrainte. Notez que cela correspond à la transposition de la matrice A dans les équations ci-dessus.
- Matrice clairsemée: pour les ensembles de contraintes plus volumineux, vous pouvez spécifier la matrice a dans sa forme Slam. Il se compose de trois champs obligatoires i, jet v, où i et j sont des index de ligne et de colonne, respectivement, et v est la valeur non nulle de l'élément Matrix. Le mode Matrice éparpillée suppose toujours l’utilisation de contraintes en lignes.
- B ancre: (obligatoire si elle n'est pas déjà fournie dans A) Utilisez cette entrée pour indiquer le nom, la direction et le côté droit des contraintes.
- contrainte: (facultatif) chaîne, nom de la contrainte.
- dir: chaîne, direction de l'inégalité de contrainte. Ce champ doit être renseigné par >=, <= ou ==.
- RHS: un nombre, le côté droit de l'inégalité, correspondant à b.
- Q ancre: optionnel. Utilisez cette entrée pour fournir la partie quadratique de la fonction objective, pour les problèmes de programmation quadratique. Il correspond à Q dans les équations. Vous pouvez la définir en tant que matrice dense ou matrice éparpillée.
- Matrice dense: les noms de champs doivent correspondre aux noms de variables de décision définis dans O.
- Matrice clairsemée: les noms de champs sont i, jet v, où i et j sont des index de ligne et de colonne, respectivement, et v est la valeur non nulle de l'élément Matrix associé.
À partir de 11,0, vous pouvez activer le mappage de champ d'affichage pour l'option d'ancrage d'entrée O pour plus de souplesse avec les noms de champs. Designer
Exemple
Si vos équations de contrainte sont: x + 2A + x + y > = 1, les éléments suivants sont tous des intrants légitimes pour l'entrée A: </bx>
Avec champ de contrainte :
| contrainte | X | y | z | |
|---|---|---|---|---|
| 1 | C1 | 1 | 2 | 3 |
| 2 | C2 | 1 | 1 | 0 |
Sans champ de contrainte :
| variable | C1 | C2 | |
|---|---|---|---|
| 1 | X | 1 | 1 |
| 2 | y | 2 | 1 |
| 3 | z | 3 | 0 |
Y compris dir et RHS:
| X | y | z | dir | rhs | |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | <= | 4 |
| 2 | 1 | 1 | 0 | >= | 1 |
L'ordre des variables pour l'entrée O et l'entrée A doit être le même.
Exemple
Ce qui suit est une entrée légitime pour l'entrée a:
| variable | C1 | C2 | |
|---|---|---|---|
| 1 | X | 1 | 1 |
| 2 | y | 2 | 1 |
| 3 | z | 3 | 0 |
À partir de 11,0, vous pouvez utiliser d'autres noms de champs pour "Constraint" ou "variable" et l'outil d'optimisation déduit intelligemment quel champ contient des contraintes et quel champ contient des variables. Cependant, la Convention de nommage est toujours préférée et recommandée.Designer
Modes d’entrée
Sélectionner le modèle comme matrices
Le mode Matrice prend en charge les matrices denses ou éparpillées(slam). Les entrées O et A sont requises pour le mode d'entrée Matrix.
Sélectionnez le type de problème:
- Programme linéaire: (par défaut) (LP) contraintes linéaires objectives et linéaires avec des variables de décision continues.
- Mixed Integer Program: (MILP) contraintes linéaires objectives et linéaires avec des variables de décision binaires ou entières ainsi que des variables de décision continues.
- Programme quadratique: (QP) contraintes quadratiques objectives et linéaires avec des variables de décision continues.
Sélectionnez Solveur:
- Glpk: (par défaut) pour les programmes linéaires et les programmes linéaires Integer mixtes
- Symphony: pour les programmes linéaires et les programmes Integer mixtes. Ce solveur est généralement plus efficace que Glpk pour les programmations MILP.
- Quadprog: pour les programmes quadratiques.
Maximiser l'objectif? : Activez cette option si vous souhaitez maximiser la fonction objective. Sinon, l’outil minimise la fonction objectif.
Sélectionner le mode contrainte pour l'ancre d'entrée A: pour plus d'informations, voir entrées.
- Matrice dense, contraintes en lignes (par défaut)
- Matrice dense, variables en lignes
- Matrice éparpillée (SLAM)
Affichage du mappage de champ pour l'ancre d'entrée o: (facultatif) l'entrée o requiert les mots réservés variable, coefficient , lb, UBou type pour les noms de champs de la table d'entrée. Si vous utilisez d’autres noms de champs ou si les noms de champs contiennent un espace vide en début ou en fin, des erreurs se produisent alors. En activant cette option, vous pouvez mapper vos champs existants aux champs variable, coefficient, lb, UBet type correspondants sans l'étape supplémentaire d'utilisation d'un Outil Sélectionner pour modifier les noms de champs.
Entrer le modèle manuellement
Ce mode offre une interface interactive dans laquelle vous pouvez définir directement les objectifs et les contraintes. L’analyse de la sensibilité est disponible en cas de problèmes de programmation linéaire.
Sélectionner le type de problème
- Programme linéaire: (LP) contraintes linéaires objectives et linéaires avec des variables de décision continues.
- Mixed Integer Program: (MILP) contraintes linéaires objectives et linéaires avec des variables de décision binaires ou entières ainsi que des variables de décision continues.
- Programme quadratique: (QP) contraintes quadratiques objectives et linéaires avec des variables de décision continues.
Sélectionnez Solveur: glpk (pour le programme linéaire et Mixed Integer Program), Symphony (pour le programme linéaire et Mixed Integer Program), ou quadprog (pour le programme quadratique).
Maximiser l'objectif? : Activez cette option s'il s'agit d'un problème de maximisation.
Liste variable: spécifiez une liste séparée par des virgules de noms de variables de décision.
Objectif: spécifier une fonction objective à maximiser ou minimiser.
Contraintes: spécifiez les contraintes. Assurez-vous que toutes les variables de la contrainte se trouvent à gauche du signe d’inégalité/égalité. (par exemple, le solveur échouera pour la contrainte 2x > = y + 4 mais s'exécutera avec succès pour la contrainte 2x-y > = 4. Bien que ces deux équations soient mathématiquement équivalentes, la deuxième satisfait aux exigences du solveur.)
Limiteset types: spécifiez les limites et les types.
Indiquer le modèle à partir d’un fichier
Ce mode prend en charge l’entrée de fichier de modèle standard.
Sélectionnez le typede fichier: CLPEX_LP, MathProgou MPS_Free.
Sélectionnez Solveur: glpk (pour le programme linéaire et Mixed Integer Program), Symphony (pour le programme linéaire et Mixed Integer Program), ou quadprog (pour le programme quadratique).
Sélectionnez fichier: spécifiez un fichier de modèle d'optimisation.
Afficher la sortie
- I ancre: cette sortie fournit un tableau de bord interactif de la solution.
- D ancre: cette sortie se compose de trois tables séparées par des tuyaux: Résumé, variableset contraintes. Ces éléments peuvent être utilisés en amont du workflow pour créer des rapports et des tableaux récapitulatifs.
- S ancre: il s'agit d'une sortie de données simple qui se compose d'une seule table avec la valeur optimale de la fonction objective et les variables de décision. En cas de problèmes consistant en des variables de décision binaires uniquement (0/1), cette table ne contient que les valeurs 1.