The Gravity Model
Adapted from Author Dr. Jean-Paul Rodrigue
Please go to the Transport Geographies Website at the following URL for more information:
http://people.hofstra.edu/geotrans/eng/ch5en/meth5en/ch5m2en.html
Elementary Formulation
The gravity model offers a good application of the spatial interaction method. It is named that way because it uses a similar formulation to Newton’s gravity model, which implies that the attraction between 2 objects is proportional to their mass and inversely proportional to their respective distance. Consequently, the general formulation of spatial interactions can be adapted to reflect this basic assumption to form the elementary formulation of the gravity model:
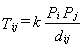
Pi and Pj are the importance of the location of origin (i ~ consumers) and the location of destination (j ~ retail establishments).
dij is the distance between the location of origin and the location of the destination.
k is a proportionality constant. Related to the rate of the event. For instance, if we consider the same system of spatial interactions, the value of k is higher if we consider interactions for a year compared to the value of k for one week. The constant is also necessary to avoid giving outputs in "squared people per square mile."
The likelihood of transactions between i and j is proportional to their attractiveness and inversely proportional to their distance.
Simple Formulation
This is a simple and much more flexible formulation of the gravity model:
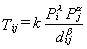
β (beta): Transport friction. Related to the efficiency of the transport system between 2 locations. Rarely linear in space, as the further the movement, the greater the friction of space. For instance, a highway between 2 locations will have a weaker beta index than a road.
λ (lambda): Potential to generate movements (emissiveness). For movements of people, often related to their welfare. For instance, if we investigate retailing movements, it's logical to infer that for an equal population, a place having higher levels of income generates more movements.
α (alpha): Potential to attract movements (attractiveness). Related to the nature of economic activities. For instance, with an equal population, a center having important commercial activities attracts more movement.
Calibration
A part of the difficulties related to the usage of spatial interaction models, notably the gravity model, is related to their calibration. Calibration consists of finding the value of parameters (constant and exponents) to ensure that the estimated results are similar to the observed flows.
Calibration is the process by which model parameters, in particular the distance decay parameter (beta) and the attractiveness power (alpha) are set in order to best represent the real-life flows observed in the market.
In the 2 formulations of the gravity model that have been presented, the simple formulation offers good flexibility for calibration since four parameters can be modified. Altering the values of beta, alpha, and lambda influences the estimated spatial interactions. Furthermore, the value of the parameters can change over time due to factors such as technological innovations and economic development. For instance, improvements in transport efficiency generally have the consequence of reducing the value of the beta exponent (friction of space).
Often, a value of 1 is given to the parameters, and then they are progressively altered until the estimated results are similar to the observed results. Calibration can also be considered for different O/D matrices according to age, income, gender, type of merchandise, and modal choice. A great part of the scientific research in transport and regional planning aims to find accurate parameters for spatial interaction equations. This is generally a costly and time-consuming process. Once a spatial interaction model has been validated for a city or a region, it can then be used for simulation and prediction purposes.