Herramienta de optimización
La herramienta de optimización soluciona la programación lineal (LP), la programación lineal de enteros mixtos (MILP) y los problemas de optimización de programación cuadrática (QP) mediante los modos de entrada matricial, manual y de archivo.
Esta herramienta utiliza la herramienta R. Ve a Opciones > Descargar herramientas predictivas e inicia sesión Portal de licencias y descargas de Alteryx para instalar R y los paquetes utilizados por la Herramienta R. Consulta Descargar y usar herramientas predictivas.
¿Qué es la optimización?
La optimización tiene aplicaciones amplias en muchas industrias, tales como cadena de suministro, transporte, servicios financieros, venta al por menor, telecomunicaciones, y energía. Las áreas de aplicación incluyen optimización de cadenas de suministro, optimización de surtidos, optimización de portafolios, programación de la fuerza laboral y programación deportiva.
Un problema de la optimización tiene típicamente la forma matemática siguiente, consistiendo en una función objetiva (primera ecuación), un sistema de restricciones (segunda ecuación), y una especificación de los tipos (continuo, entero, binario) y límites de la decisión variables (tercera ecuación). El objetivo suele ser encontrar los valores de las variables de decisión que maximizan o minimizan el objetivo, a la vez que satisfacen todas las restricciones subyacentes, tipos y límites.
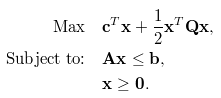
Conectar entradas
No se requieren entradas para los modos de entrada manual o de archivo. Para el modo de entrada de la matriz, las entradas o y a son necesarias, pero B y Q son opcionales.
- O ancla: (requerido para el modo de entrada de matriz) Utilice esta entrada para proporcionar los nombres de las variables de decisión, sus coeficientes en la función objetiva y, opcionalmente, sus límites y tipos.
- variable: (requerido) una cadena, nombres de variables de decisión. Corresponde a x en las ecuaciones.
- coeficiente: (requerido) un número, coeficiente de cada variable de la decisión en la función objetiva. Corresponde a c.
- lb: (opcional) un número, límite inferior de la variable de decisión. El valor predeterminado es 0.
- UB: (opcional) un número, límite superior de la variable de decisión. El valor predeterminado es INF (infinito positivo).
- Escriba: (opcional) un carácter, el tipo de la variable de decisión, que puede ser C (continuo), B (binario), o I (entero). El valor por defecto es C.
- A ancla: (requerido para el modo de entrada de matriz) Utilice esta entrada para proporcionar la matriz de restricción correspondiente a a en las ecuaciones. Puede organizar la matriz de dos maneras diferentes:
- Matriz densa:
- Restricciones en filas: cada fila corresponde a una restricción. Opcionalmente, el primer campo puede denominarse restricción para indicar el nombre de restricción en cada fila, mientras que los nombres de campo restantes deben corresponder a las variables de decisión definidas en O. Además, puede incluir los campos dir y RHS para rodar la entrada B en este.
- Variables en filas: cada fila corresponde a una variable. El primer campo debe denominarse variable, mientras que los nombres de campo restantes deben corresponder a los nombres de restricción. Tenga en cuenta que esto corresponde a la transpuesta de la matriz a en las ecuaciones anteriores.
- Matriz dispersa: para conjuntos de restricción más grandes, puede especificar la matriz a en su forma Slam. Consta de tres campos requeridos i, jy v, donde i y j son índices de fila y columna, respectivamente, y v es el valor distinto de cero del elemento Matrix. El modo de matriz dispersa siempre asume restricciones en filas.
- B anclaje: (requerido si no se ha proporcionado en a) Utilice esta entrada para proporcionar el nombre, dirección y lado derecho de las restricciones.
- restricción: (opcional) una cadena, nombre de la restricción.
- DIR: una cadena, dirección de la desigualdad de restricción. Tiene que ser > =,</= or ==.>
- RHS: un número, el lado derecho de la desigualdad, correspondiente a b.
- ancla Q: opcional. Utilice esta entrada para proporcionar la parte cuadrática de la función objetiva, para problemas de programación cuadrática. Corresponde a Q en las ecuaciones. Puede especificarla como una matriz densa o como una matriz dispersa.
- Matriz densa: los nombres de campo deben corresponder a los nombres de las variables de decisión definidas en O.
- Matriz dispersa: los nombres de campo son i, jy v, donde i y j son índices de fila y columna, respectivamente, y v es el valor distinto de cero del elemento de matriz asociado.
Comenzando con 11,0, puede habilitar la asignación de campo de visualización para la opción ancla de entrada O para mayor flexibilidad con los nombres de campo. Designer
Ejemplo
Si sus ecuaciones de restricción son: x + 2Y + x + y > = 1, las siguientes son todas las entradas legítimas para la entrada a: </bx>
Con el campo restricción:
| restricción | x | y | Z | |
|---|---|---|---|---|
| 1 | C1 | 1 | 2 | 3 |
| 2 | C2 | 1 | 1 | 0 |
Sin campo de restricción:
| variable | C1 | C2 | |
|---|---|---|---|
| 1 | x | 1 | 1 |
| 2 | y | 2 | 1 |
| 3 | Z | 3 | 0 |
Incluyendo dir y RHS:
| x | y | Z | dir | rhs | |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | <= | 4 |
| 2 | 1 | 1 | 0 | >= | 1 |
El orden de las variables para la entrada o y la entrada A debe ser el mismo.
Ejemplo
Lo siguiente es una entrada legítima para la entrada a:
| variable | C1 | C2 | |
|---|---|---|---|
| 1 | x | 1 | 1 |
| 2 | y | 2 | 1 |
| 3 | Z | 3 | 0 |
A partir de 11,0, puede utilizar otros nombres de campo para "restricción" o "variable" y la herramienta de optimización deduce inteligentemente qué campo contiene restricciones y qué campo contiene variables. Sin embargo, la Convención de nomenclatura sigue siendo preferida y recomendada.Designer
Modos de entrada
Seleccione el modelo como matrices
El modo Matrix admite matrices densas o escasas (Slam). Las entradas o y a son necesarias para el modo de entrada matricial.
Seleccione el tipo de problema:
- Programa lineal: (por defecto) (LP) objetivos lineales y restricciones lineales con variables de decisión continuas.
- Programa entero mixto: (MILP) limitaciones lineales objetivas y lineales con variables de decisión binarias o enteras junto con variables de decisión continuas.
- Programa cuadrático: (QP) las restricciones objetivas y lineales cuadráticas con variables de decisión continuas.
Seleccione Solver:
- GLPK: (predeterminado) para programas lineales y programas lineales enteros mixtos
- Sinfonía: para programas lineales y programas enteros mixtos. Normalmente funciona mejor que GLPK para MILP.
- Quadprog: para programas cuadráticos.
Maximizar objetivo? : Habilite esta opción si desea maximizar la función objetiva. De lo contrario, la herramienta minimiza la función objetiva.
Seleccione el modo de restricción para el ancla de entrada a: para obtener más información, consulte entradas.
- Matriz densa, restricciones en filas (por defecto)
- Matriz densa, variables en columna
- Matriz poco densa (SLAM)
Asignación de campo de visualización para el anclaje de entrada o: (opcional) la entrada o requiere las palabras reservadas variable, coeficiente , lb, UBo tipo para los nombres de campo de la tabla de entrada. Si utiliza distintos nombres de campo, o si los nombres de campo contienen espacio en blanco interlineado o posterior, se producen errores. Al activar esta opción, puede asignar los campos existentes a los campos variables, coeficientes, lb, UBy tipo correspondientes sin el paso adicional de usar un Herramienta Seleccionar para cambiar los nombres de los campos.
Introducir el modelo manualmente
Este modo ofrece una interfaz interactiva donde puede especificar objetivos y restricciones directamente. El análisis de sensibilidad está disponible para problemas de programación lineal.
Seleccionar el tipo de problema
- Programa lineal: (LP) objetivos lineales y restricciones lineales con variables de decisión continuas.
- Programa entero mixto: (MILP) limitaciones lineales objetivas y lineales con variables de decisión binarias o enteras junto con variables de decisión continuas.
- Programa cuadrático: (QP) las restricciones objetivas y lineales cuadráticas con variables de decisión continuas.
Seleccione Solver: GLPK (programa lineal y programa entero mixto), Sinfonía (para programa lineal y programa entero mixto), o Quadprog (para programa cuadrático).
Maximizar objetivo? : Habilite esta opción si se trata de un problema de maximización.
Listade variables: especifique una lista separada por comas de nombres de variables de decisión.
Objetivo: especifique una función objetiva para maximizarla o minimizarla.
Restricciones: especifique las restricciones. Asegúrese de que todas las variables de la restricción estén en el lado izquierdo del signo de desigualdad/igualdad. (por ejemplo, Solver fallará por restricción 2x > = y + 4 pero se ejecutará satisfactoriamente para la restricción 2x-y > = 4. Aunque ambas ecuaciones son matemáticamente equivalentes, la segunda cumple con los requisitos del solucionador.)
Límitesy tipos: especifique los límites y los tipos.
Especificar el modelo desde un archivo
Este modo admite la entrada del archivo de modelo estándar de la industria.
Seleccione tipode archivo: CLPEX_LP, MathProgo MPS_Free.
Seleccione Solver: GLPK (programa lineal y programa entero mixto), Sinfonía (para programa lineal y programa entero mixto), o Quadprog (para programa cuadrático).
Seleccione archivo: especifique un archivo de modelo de optimización.
Ver la salida
- I Anchor: esta salida proporciona un panel interactivo de la solución.
- D ancla: esta salida consta de tres tablas separadas por tuberías: Resumen, variablesy restricciones. Se pueden utilizar de forma ascendente en el flujo de trabajo para crear informes y Dashboards.
- S ancla: se trata de una salida de datos simple que consiste en una única tabla con el valor óptimo de la función objetiva y las variables de decisión. Para los problemas que consisten solamente en variables de decisión binarias (0/1), esta tabla contiene sólo aquellos valores que son 1.