Lo strumento Ottimizzazione risolve problemi relativi alla programmazione lineare (LP), alla programmazione lineare mista-intera (MILP) e alla programmazione quadratica (QP) usando la modalità matrice, manuale e input file.
Questo strumento utilizza lo strumento R. Vai a Opzioni > Scarica strumenti predittivi e accedi al portale Download e licenze Alteryx per installare R e i pacchetti utilizzati dallo strumento R. Per ulteriori informazioni, consulta la sezione Download e utilizzo degli strumenti predittivi.
L'ottimizzazione ha ampie applicazioni in molti settori, come la catena di approvvigionamento, i trasporti, i servizi finanziari, la vendita al dettaglio, le telecomunicazioni e l'energia. Le aree di applicazione includono l'ottimizzazione della catena di approvvigionamento, l'ottimizzazione dell'assortimento, l'ottimizzazione del portafoglio, la pianificazione della forza lavoro e la pianificazione dello sport.
Un problema di ottimizzazione ha in genere la seguente forma matematica, costituita da una funzione obiettivo (1a equazione), un insieme di vincoli (2a equazione), e una specifica dei tipi (continuo, intero, binario) e dei limiti delle variabili di decisione (3a equazione). L'obiettivo è in genere quello di trovare i valori delle variabili decisionali che massimizzano o riducono al minimo l'obiettivo, soddisfacendo al contempo tutti i vincoli, i tipi e i limiti sottostanti.
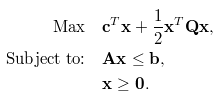
Non sono richiesti input per le modalità di input manuale o file. Per la modalità di input matrice, sono richiesti gli input O e A, ma B e Q sono facoltativi. L'input B è facoltativo solo in alcuni casi. Non è sempre possibile fornire le informazioni nell'input A, solo se sono stati selezionati vincoli nelle righe.
Ancoraggio O: (richiesto per la modalità di input matrice) utilizza questo input per fornire i nomi delle variabili di decisione, i loro coefficienti nella funzione obiettivo e, facoltativamente, i loro limiti e tipi.
A causa della funzionalità R, i nomi dei campi distinguono tra maiuscole e minuscole. A partire da Designer 11.0, è possibile attivare l'opzione Visualizza campo mappando gli Ancoraggi di input O per una maggiore flessibilità con i nomi dei campi.
variabile (obbligatoria): una stringa, nomi di variabili decisionali. Corrisponde a x nelle equazioni.
coefficiente (obbligatorio): un numero, coefficiente di ciascuna variabile di decisione nella funzione oggettiva. Corrisponde a c.
lb (facoltativo): un numero, limite inferiore della variabile di decisione. Il valore predefinito è 0.
ub (facoltativo): un numero, limite superiore della variabile di decisione. Il valore predefinito è Inf (infinito positivo).
tipo (facoltativo): un carattere, il tipo della variabile decisionale, che può essere C (continuo), B (binario) o I (intero). Il valore predefinito è C.
Ancoraggio A (obbligatorio per la modalità di input matrice): utilizza questo input per fornire la matrice del vincolo corrispondente ad A nelle equazioni. È possibile organizzare la matrice in due modi diversi:
Matrice densa:
Vincoli nelle righe: ogni riga corrisponde a un vincolo.
Il primo campo può essere chiamato come vincolo per indicare il nome del vincolo in ogni riga, mentre i restanti nomi dei campi devono corrispondere alle variabili decisionali definite in O.
Inoltre, è possibile includere i campi dir e rhs per combinare l'input B nell'input A.
dir: una stringa, direzione della disuguaglianza del vincolo. Deve essere >=, <= o ==.
rhs: un numero, il lato destro della disuguaglianza, corrispondente alla lettera b.
I campi delle variabili (x, y e z nell'esempio seguente) devono essere numerici.
L'ordine delle colonne deve corrispondere all'ordine delle righe per l'input O.
Esempio: se le equazioni del vincolo sono: x + 2y + 3z <= 4 e x + y >= 1, questi sono tutti input legittimi per l'input A:
Con campo di vincolo:
vincolo
x
y
z
1
c1
1
2
3
2
c2
1
1
0
Senza campo di vincolo:
x
y
z
1
1
2
3
2
1
1
0
Inclusi dir e rhs:
x
y
z
dir
rhs
1
1
2
3
<=
4
2
1
1
0
>=
1
Variabili in righe: ogni riga corrisponde a una variabile.
Il primo campo dovrebbe essere denominato variabile, mentre i restanti nomi dei campi dovrebbero corrispondere ai nomi dei vincoli. Si noti che questo corrisponde alla trasposizione della matrice A nelle equazioni precedenti.
I campi di vincolo (c1 e c2 nell'esempio seguente) devono essere numerici.
L'ordine delle variabili per l'input O e l'input Adeve essere lo stesso.
Esempio: si tratta di un input legittimo per l'input A:
variabile
c1
c2
1
x
1
1
2
y
2
1
3
z
3
0
A partire da Designer 11.0, è possibile utilizzare altri nomi di campo per "vincolo" o "variabile"; Strumento Ottimizzazione deduce in modo intelligente quale campo contiene vincoli e quale campo contiene variabili. Tuttavia, la convenzione di denominazione è ancora preferita e raccomandata.
Matrice sparsa: per gruppi di vincoli più grandi, è possibile specificare la matrice A nella sua forma SLAM. È costituito da 3 campi obbligatori i, j, e v, dove i e j sono rispettivamente indici di riga e di colonna, e v è il valore diverso da zero dell'elemento matrice. La modalità a matrice sparsa presuppone sempre i vincoli nelle righe.
Ancoraggio B (obbligatorio se non già fornito in A): utilizza questo input per fornire il nome, la direzione e il lato destro dei vincoli.
constraint (facoltativo): una stringa, nome del vincolo.
dir: una stringa, direzione della disuguaglianza del vincolo. Deve essere >=, <= o ==.
rhs: un numero, il lato destro della disuguaglianza, corrispondente alla lettera b.
Ancoraggio Q (facoltativo): utilizza questo input per fornire la porzione quadratica della funzione obiettivo, per i problemi di programmazione quadratica. Corrisponde a Q nelle equazioni. È possibile specificarlo come matrice densa o matrice sparsa.
Matrice densa: i nomi dei campi devono corrispondere ai nomi delle variabili decisionali definiti in O.
Matrice sparsa: i nomi dei campi sono i, j, e v, dove i e j sono rispettivamente indici di riga e di colonna, e v è il valore diverso da zero dell'elemento matrice associato.
La modalità Matrice supporta matrici dense o sparse (SLAM). Gli input O e A sono necessari per la modalità di input matrice.
Seleziona il tipo di problema:
Programma lineare: (predefinito)(LP) vincoli lineari oggettivi e lineari con variabili decisionali continue.
Mixed Integer Program: (MILP) vincoli lineari oggettivi e lineari con variabili di decisione binarie o intere insieme a variabili di decisione continue.
Programma quadratico: (QP) vincoli quadratici oggettivi e lineari con variabili decisionali continue.
Seleziona risolutore:
Glpk: (predefinito) per i programmi lineari e i programmi lineari interi misti.
Symphony: per i programmi lineari e i programmi misti interi. Di solito funziona meglio di Glpk per MILP.
Quadprog: per i programmi quadratici.
Massimizzare l'obiettivo?: attiva questa opzione se vuoi massimizzare la funzione obiettivo. In caso contrario, lo strumento riduce al minimo la funzione obiettivo.
Seleziona modalità vincolata per l'ancoraggio di input A: per i dettagli, fai riferimento a Connetti input sopra.
Matrice alta densità, vincoli nelle righe (predefinito)
Matrice alta densità, variabili nelle righe
Matrice sparsa (SLAM)
Visualizza campo mappando gli ancoraggi di input A(facoltativo): l'input O richiede le parole riservate variabile, coefficiente, lb, ub o tipo per i nomi dei campi della tabella di input. Se utilizzi nomi di campo diversi o se i nomi di campo contengono spazi vuoti iniziali o finali, si verificano errori. Attivando questa opzione, puoi mappare i campi esistenti ai campi variabile, coefficiente, lb, ub e tipo corrispondenti senza la procedura aggiuntiva di utilizzare un Strumento Seleziona per modificare i nomi di campo.
Questa modalità offre un'interfaccia interattiva in cui è possibile specificare direttamente obiettivi e vincoli. L'analisi della sensibilità è disponibile per problemi di programmazione lineare.
Seleziona il tipo di problema:
Programma lineare: (LP) vincoli lineari oggettivi e lineari con variabili decisionali continue.
Mixed Integer Program: (MILP) vincoli lineari oggettivi e lineari con variabili di decisione binarie o intere insieme a variabili di decisione continue.
Programma quadratico: (QP) vincoli quadratici oggettivi e lineari con variabili decisionali continue.
Seleziona risolutore: Glpk (per i programmi lineari e i programmi misti interi), Symphony (per i programmi lineari e i programmi misti interi) o Quadprog (per i programmi quadratici).
Massimizzare l'obiettivo?: attiva questa opzione se si tratta di un problema di massimizzazione.
Elenco variabili: specifica un elenco separato da virgole dei nomi delle variabili decisionali.
Obiettivo: specifica una funzione obiettivo da massimizzare o ridurre al minimo.
Vincoli: specifica i vincoli. Assicurati che tutte le variabili nel vincolo siano sul lato sinistro del segno di disuguaglianza/uguaglianza. (Ad esempio, il risolutore non viene eseguito per il vincolo 2x>=y+4 ma viene eseguito correttamente per il vincolo 2x-y>=4. Sebbene entrambe le equazioni siano matematicamente equivalenti, la seconda soddisfa i requisiti del risolutore.)
Limiti e tipi: specifica i limiti e i tipi.
Questa modalità supporta l'input di file modello standard del settore.
Seleziona il tipo di file: CLPEX_LP, MathProg o MPS_Free.
Seleziona risolutore: Glpk (per i programmi lineari e i programmi misti interi), Symphony (per i programmi lineari e i programmi misti interi) o Quadprog (per i programmi quadratici).
Seleziona file: specifica un file di modello di ottimizzazione.
Ancoraggio I: questo output fornisce un dashboard interattivo della soluzione.
Ancoraggio D: questo output è costituito da 3 tabelle separate da barre verticali: riepilogo, variabili e vincoli. Possono essere utilizzati a monte nel flusso di lavoro per creare report e dashboard.
Ancoraggio S: si tratta di un semplice output di dati che consiste in una singola tabella con il valore ottimale della funzione obiettivo e delle variabili decisionali. Per i problemi costituiti solo da variabili decisionali binarie (0/1), questa tabella contiene solo i valori pari a 1.

