A ferramenta Otimização resolve problemas de otimização de programação linear (LP, linear programming), programação inteira mista (MILP, mixed-integer linear programming) e programação quadrática (QP, quadratic programming) usando os modos de entrada manual, por matriz e por arquivo.
Essa ferramenta utiliza a ferramenta R. Vá para Opções > Baixar ferramentas preditivas e faça login no Portal de Downloads e Licenças da Alteryx para instalar o R e os pacotes usados pela ferramenta R. Acesse Baixar e utilizar ferramentas Preditivas para obter mais informações.
A otimização é amplamente adotada em muitos setores, como supply chain (cadeia de fornecimento), transportes, serviços financeiros, varejo, telecomunicações e energia. As áreas de uso incluem otimização de supply chain, sortimento e portfólio e programação da força de trabalho e desportiva.
Normalmente, um problema de otimização tem o seguinte formato matemático, que consiste em uma função objetiva (primeira equação), um conjunto de restrições (segunda equação), uma especificação dos tipos (contínuo, inteiro, binário) e limites das variáveis de decisão (terceira equação). Em geral, o objetivo é encontrar os valores das variáveis de decisão que maximizam ou minimizam o objetivo e cumprir todas as restrições, os tipos e os limites subjacentes.
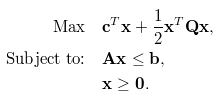
Não são necessárias entradas para os modos manual ou de arquivo. Para o modo de entrada de matriz, as entradas O e A são obrigatórias, mas B e Q são opcionais. A entrada B é opcional apenas em alguns casos. Nem sempre é possível inserir as informações na entrada A, apenas se você selecionou restrições em linhas.
Âncora O (obrigatória para o modo de entrada de matriz): use esta entrada para inserir os nomes das variáveis de decisão, seus coeficientes na função objetiva e, opcionalmente, os limites e os tipos.
Devido à funcionalidade do R, observe que os nomes dos campos diferenciam maiúsculas de minúsculas. A partir do Designer 11.0, você pode habilitar a opção "Mostrar mapeamento de campos para a âncora de entrada O" para obter mais flexibilidade com os nomes de campos.
variável (Obrigatória): uma cadeia de caracteres (string), nomes de variáveis de decisão. Corresponde a x nas equações.
coeficiente (Obrigatório): um número, coeficiente de cada variável de decisão na função objetiva. Corresponde a c.
lb(Opcional) : um número, limite mínimo da variável de decisão. O valor padrão é 0.
ub (Opcional): um número, limite máximo da variável de decisão. O valor padrão é Inf (infinito positivo).
tipo (Opcional): um caractere, o tipo da variável de decisão, que pode ser C (contínuo), B (binário) ou I (inteiro). O valor padrão é C.
Âncora A (obrigatória para o modo de entrada de matriz): use esta entrada para fornecer a matriz de restrição correspondente a A nas equações. Você pode organizar a matriz de duas formas diferentes:
Matriz densa:
Restrições em linhas: cada linha corresponde a uma restrição.
O primeiro campo pode ser chamado de restrição para indicar o nome da restrição em cada linha. Os nomes dos campos restantes devem corresponder às variáveis de decisão definidas em O.
Você também pode incluir os campos dir e rhs para combinar a entrada B com a entrada A.
dir: uma cadeia de caracteres (string), direção da restrição de desigualdade. Esse valor deve ser >=, <= ou ==.
rhs: um número, o lado direito da desigualdade, correspondente a b.
Os campos de variável (x, y e z no exemplo abaixo) devem ser numéricos.
A ordem das colunas deve corresponder à ordem das linhas na entrada O.
Exemplo: se as equações de restrição são: x + 2y + 3z <= 4 e x + y >= 1, elas são todas entradas legítimas para a entrada A:
Com campo de restrição:
restrição
x
y
z
1
c1 (cinza rodovias principais 2)
1
2
3
2
c2 (cinza rodovias principais 2)
1
1
0
Sem campo de restrição:
x
y
z
1
1
2
3
2
1
1
0
Incluindo dir e rhs:
x
y
z
dir
rhs
1
1
2
3
<=
4
2
1
1
0
>=
1
Variáveis em linhas: cada linha corresponde a uma variável.
O primeiro campo deve ser chamado variável. Os nomes dos campos restantes devem corresponder aos nomes das restrições. Observe que isso corresponde à transposição da matriz A nas equações acima.
Os campos de restrição (c1 e c2 no exemplo abaixo) devem ser numéricos.
A ordem das variáveis para as entradas O e Adeve ser igual.
Exemplo: esta é uma entrada legítima para A:
variável
c1 (cinza rodovias principais 2)
c2 (cinza rodovias principais 2)
1
x
1
1
2
y
2
1
3
z
3
0
A partir do Designer 11.0, você pode usar outros nomes de campos para "restrição" ou "variável", e a ferramenta Otimização deduz de maneira inteligente o campo que contém as restrições e o campo que contém as variáveis. No entanto, a convenção de nomenclatura ainda é preferida e recomendada.
Matriz esparsa: para conjuntos de restrições maiores, você pode especificar a matriz A no formato SLAM. Isso consiste em três campos obrigatórios i, j e v, em que i e j são os índices de linha e de coluna, respectivamente, e v é o valor diferente de zero do elemento de matriz. O modo de matriz esparsa sempre assume as restrições em linhas.
Âncora B (obrigatória se ainda não foi inserida em A): use esta entrada para especificar o nome, a direção e o lado direito das restrições.
restrição (Opcional): uma cadeia de caracteres (string), nome da restrição.
dir: uma cadeia de caracteres (string), direção da restrição de desigualdade. Esse valor deve ser >=, <= ou ==.
rhs: um número, o lado direito da desigualdade, correspondente a b.
Âncora Q (opcional): use esta entrada para inserir a parte quadrática da função objetiva, no caso de problemas de programação quadrática. Corresponde a Q nas equações. Você pode especificá-la como uma matriz densa ou esparsa.
Matriz densa: os nomes dos campos devem corresponder aos nomes das variáveis de decisão definidos em O.
Matriz esparsa: os nomes dos campos são i, j e v, em que i e j são os índices de linha e de coluna, respectivamente, e v é o valor diferente de zero do elemento de matriz associado.
O modelo de matriz é compatível com matrizes densas ou esparsas (slam). As entradas O e A são obrigatórias para o modelo de entrada de matriz.
Selecionar tipo de problema:
Programação linear (padrão) (LP): restrições lineares e objetivas lineares com variáveis de decisão contínuas.
Programação inteira mista (MILP): restrições lineares e objetivas lineares com variáveis de decisão binárias ou inteiras junto com variáveis de decisão contínuas.
Programação quadrática (QP): restrições lineares e objetivas quadráticas com variáveis de decisão contínuas.
Selecionar solucionador:
Glpk (padrão): para programações lineares e programações lineares inteiras mistas.
Symphony: para programações lineares e programações inteiras mistas. Ele geralmente apresenta um desempenho melhor do que o Glpk para MILP.
Quadprog: para programações quadráticas.
Maximizar objetivo?: habilite essa opção se quiser maximizar a função objetiva. Caso contrário, a ferramenta minimizará a função objetiva.
Selecionar modo de restrição para a âncora de entrada A: para obter detalhes, consulte "Conectar entradas" acima.
Matriz densa, restrições em linhas (padrão)
Matriz densa, variáveis em linhas
Matriz esparsa (SLAM)
Mostrar mapeamento de campo para a âncora de entrada O (opcional): a entrada O requer as palavras reservadas variável, coeficiente, lb, ub ou tipo para os nomes dos campos da tabela de entrada. Se você usar outros nomes de campos ou se os nomes de campos contiverem espaço em branco à esquerda ou à direita, haverá erros. Habilite essa opção para você mapear seus campos existentes para os campos correspondentes variável, coeficiente, lb, ub e tipo sem o passo adicional de usar uma ferramenta Selecionar para alterar os nomes dos campos.
Este modo oferece uma interface interativa na qual você pode especificar objetivos e restrições diretamente. A análise de sensibilidade está disponível para problemas de programação linear.
Selecionar tipo de problema:
Programação linear (LP): restrições lineares e objetivas lineares com variáveis de decisão contínuas.
Programação inteira mista (MILP): restrições lineares e objetivas lineares com variáveis de decisão binárias ou inteiras junto com variáveis de decisão contínuas.
Programação quadrática (QP): restrições lineares e objetivas quadráticas com variáveis de decisão contínuas.
Selecionar solucionador: Glpk (para Programação linear e Programação inteira mista), Symphony (para Programação linear e Programação inteira mista) ou Quadprog (para Programação quadrática).
Maximizar objetivo?: habilite essa opção se este for um problema de maximização.
Lista de variáveis: especifique uma lista separada por vírgula de nomes de variáveis de decisão.
Objetivo: especifique uma função objetiva para ser maximizada ou minimizada.
Restrições: especifique as restrições. Garanta que todas as variáveis na restrição estejam do lado esquerdo do sinal de desigualdade/igualdade. (Por exemplo, há uma falha no solucionador para a restrição 2x>=y+4, mas ele é bem-sucedido para a restrição 2x-y>=4. As duas equações são matematicamente equivalentes, mas a segunda cumpre os requisitos do solucionador.)
Limites e tipos: especifique os limites e os tipos.
Este modo é compatível com a entrada de arquivos de modelo padrão do setor.
Selecionar tipo de arquivo: CLPEX_LP, MathProg ou MPS_Free.
Selecionar solucionador: Glpk (para Programação linear e Programação inteira mista), Symphony (para Programação linear e Programação inteira mista) ou Quadprog (para Programação quadrática).
Selecionar arquivo: especifique um arquivo de modelo de otimização.
Âncora I: esta saída apresenta um painel interativo da solução.
Âncora D: esta saída consiste em três tabelas separadas por barra vertical: resumo, variáveis e restrições. Elas podem ser usadas em etapas anteriores no fluxo de trabalho para criar relatórios e painéis.
Âncora S: esta é uma saída de dados simples que consiste em uma única tabela com o valor ideal da função objetiva e das variáveis de decisão. Para problemas que consistem apenas em variáveis de decisão binárias (0/1), esta tabela contém apenas os valores que são 1.

